概述
数据结构要素
- 数据的逻辑结构:线性结构(数组、栈、队列、链表)、非线性结构、集合、图等。
- 数据的存储结构:顺序存储(数组)、链式存储、索引存储、散列存储等。
- 数据的运算:初始化、判空、统计、查找、遍历、插入、删除、更新等。
常见的数据结构
- 数组
- 链表
- 栈
- 队列
- 树
- 二叉树
- 集合
- 哈希
- 堆
- 优先队列
并查集
并查集 - OI Wiki主要用于处理一些不相交集合的合并问题。如连通子图、最小生成树Kruskal算法、最近公共祖先(Lowest Common Ancestors, LCA)等。
规定
规定数组a[],若i的祖先是x,则a[i] == x,特别的,如i就是最高的祖先,则a[i] == i。
初始化
建立数组[i],并赋值a[i] = i
合并
优化后,时间复杂度$\log_2n$
递归查找到a和b的祖先,找到之后,将其中一个的祖先设置为另一个祖先的儿子。这可能导致查找树的退化(某一条支路太长,退化成链表),解决方案是引入height[]数组记录每个祖先的高度,合并时将矮的树合并到高的树上。
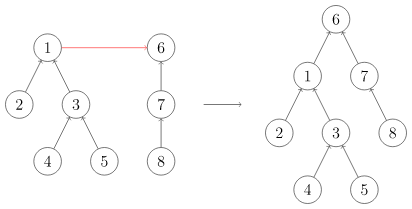
优化后,时间复杂度为$\log_2n$
递归向上查找祖先可能导致查询次数太多。优化方式是执行一次查询后,就直接将返回的祖先结果赋值为该值的直接祖先,下次搜索的时间复杂度可达$O(1)$。
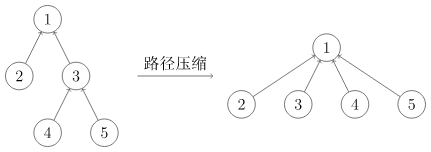
二叉树
相关知识已经在严蔚敏的《数据结构》中学习。
书上有一道没见过的题目:
基础题目
输入二叉树的先序和中序遍历,求后序遍历。
- 输入样例。 先序:1 2 4 7 3 5 8 9 6 中序:4 7 2 1 8 5 9 3 6
- 输出样例。 后序:7 4 2 8 9 5 6 3 1
思路
将先序序列和中序序列存入数组。先序序列中的第一个数字1为根节点,因此中序序列中,1左侧的均在根节点的左孩子上,1右侧的均在根节点的右孩子上。根据上述描述,不断缩小区间,递归完成建树任务。然后后序遍历二叉树即可输出后序序列。
代码实现
#pragma warning(disable:4996)
#include <bits/stdc++.h>
using namespace std;
#define MAX_LENGTH 100
typedef struct Node {
int data;
Node* L, * R;
}bitNode,* bitTree; // 二叉链表
int pre[MAX_LENGTH], in[MAX_LENGTH];
int length = 0;
int pp = 0; // 记录当前先序序列元素下标
// 建树,s是in数组下标起点,e是in数组下标终点
bitTree buildTree(int s, int e) {
if (s > e) {
return NULL;
}
bitTree node = (bitTree)malloc(sizeof(bitNode));
node->data = pre[pp]; // 先序第一个是根节点
int i; // 当前元素在中序序列中的下标
for (i = s; i <= e; i++) {
if (pre[pp] == in[i]) {
break;
}
}
pp++;
node->L = buildTree(s, i - 1);
node->R = buildTree(i + 1, e);
return node;
}
// 后序遍历
void suffTra(bitNode* tree) {
if (tree == NULL) {
return;
}
suffTra(tree->L);
suffTra(tree->R);
printf("%d ", tree->data);
}
int main() {
// 读入数据
cout << "先序: ";
int i = 0;
while (1) {
char a;
scanf("%c", &a);
if (a == '\n') {
break;
}
else if (a == 32) {
continue;
}
pre[i] = (int)(a - '0');
i++;
}
length = i;
cout << "中序: ";
for (i = 0; i < length; i++) {
scanf("%d", in + i);
}
// 建树
bitNode* bt = buildTree(0, length - 1);
// 后序遍历
cout << "后序: ";
suffTra(bt);
cout << endl;
}总结反思
思路和书本一致,因此代码居然也很像。不过我数据读入部分真的写的很烂,书上又没有完全按照题目要求来写,所以下次有机会再学习改善吧……
一个不太重要的小tip,就是标准情况下应该在程序运行结束之前释放所有二叉树节点所占空间,否则会导致内存泄漏。
最后,学习一下new关键字。new关键字不仅可以像malloc一样动态分配内存空间,同时还创建了对象。 书上的结构体定义很神奇:
typedef struct Node {
int data;
Node* L, * R;
Node(int data = 0, Node* L = NULL, Node* R = NULL):data(data),L(L),R(R){}
}bitNode,* bitTree;它能给结构体变量赋初值,Node test就能获得一个data=0, L==R==NULL的test变量。 当new一个Node的时候,可以获得一个data初值为0,左右孩子初值为NULL的Node。 冒号后面的data(data),L(L),R(R)似乎还定义了构造函数,可以在new的时候赋初值,
Node b;
Node* test = new Node(5, &b, &b);获得一个data为0,左右孩子均指向b的Node。构造函数参数可以省略一部分,从左到右依次读入data,L,R。如果删掉R(R),,则无法为右孩子赋初值。 这部分知识以后再学习,现在先拿来用。
二叉搜索树
已经在严蔚敏《数据结构》中学习,稍微困难一些的地方是插入和删除元素要做的操作。 STL中的set和map是用二叉搜索树(红黑树)实现的,检索和更新复杂度是$\log_2n$。见:ACM笔记 – STL和基本数据结构
搭mc服务器去了~明天再看 13天后,终于到了“明天”,这段时间摆大烂了😁
( ̄y▽, ̄)╭
特点
- 每个元素有唯一的键值,键值间能比较大小
- 任意一个结点的键值,大于左子树小于右子树,因此可以用递归的思想来定义二叉搜索树。
Treap树
Tree Heap,Treap是树和堆的结合。 OI Wiki: https://oi-wiki.org/ds/treap/
性质
- 每个节点有一个键值,还有一个优先级。
- 对键值来说,这棵树是二叉排序树;对优先级来说,这棵树是大顶堆。
插入
先按照键值大小插入,然后判断优先级是否满足要求。调整优先级的方式类似ASL的左旋右旋。书上的代码写的很精彩。
// d = 0为坐旋转, d = 1为右旋转
void rotate(Node* &o, int d){
Node* K = o->son[d^1];
o->son[d^1]=k->son[d];
k->son[d]=o;
o=k;
}Node* &o,相当于传了o指针的指针- 位运算
d^1与1-d等价,但速度更快
找到旋转的特点,用一个函数搞定左旋右旋。
删除
将要删除的节点旋转成叶子,然后直接删去。
分裂与合并
暂未研究
Treap与名次树
HDU 4585
STL
#pragma warning(disable:4996)
#include <bits/stdc++.h>
using namespace std;
map<int, int> mp; // first是等级,second是id
int main() {
mp[1000000000] = 1;
int n;
scanf("%d", &n);
while (n--) {
int id, le;
scanf("%d %d", &id, &le);
mp[le] = id;
int ans;
map<int, int>::iterator it = mp.find(le);
if (it == mp.begin()) {
ans = (++it)->second;
}
else
{
map<int, int>::iterator it2 = it;
it2++;
it--;
ans = it2->first - le < it->second - le ? it2->second : it->second;
}
printf("%d %d", id, ans);
}
}
++运算优先级低于->
.
Treap树
线段树
POJ 2182暴力解法:
#include <iostream>
using namespace std;
#define MAX 8010
int main() {
int a[MAX]; // 输入
int b[MAX]; // 辅助
int c[MAX]; // 输出
int n;
cin >> n;
a[0] = 0;
b[0] = 1;
for (int i = 1; i < n; i++) {
cin >> a[i];
b[i] = i + 1;
}
for (int i = n - 1; i >= 0; i--) {
int t = a[i];
for (int j = 0; j < n; j++) {
if (t == 0 && b[j] != 0) {
c[i] = b[j];
b[j] = 0;
break;
}
if (b[j] != 0) {
t--;
}
}
}
for (int i = 0; i < n; i++) {
cout << c[i] << endl;
}
}寻找每一位数都要遍历整个数组,时间复杂度$O^2$,在POJ显示用时516MS。为了少遍历一些数,采用线段树的方法,可以将复杂度提升至$n\log n$。优化后的运行时间为125MS。
#include <iostream>
using namespace std;
#define MAX 8010
typedef struct Tree {
int start, end, total;
}tree;
tree t[40000];
void buildTree(int start, int end, int n) {
t[n] = { start, end, end - start + 1 };
if (start == end) {
return;
}
buildTree(start, (start + end) / 2, 2 * n);
buildTree((start + end) / 2 + 1, end, 2 * n + 1);
}
int query(int pre, int n) {
t[n].total--;
if (t[n].start == t[n].end) {
return t[n].start;
}
if (pre > t[2 * n].total) {
return query(pre - t[2 * n].total, 2 * n + 1);
}
return query(pre, 2 * n);
}
int main() {
int a[MAX]; // 输入
int c[MAX]; // 输出
int n;
cin >> n;
a[0] = 0;
for (int i = 1; i < n; i++) {
cin >> a[i];
}
buildTree(1, n, 1);
for (int i = n - 1; i >= 0; i--) {
c[i] = query(a[i] + 1, 1);
}
for (int i = 0; i < n; i++) {
cout << c[i] << endl;
}
}