基本算术的实现

加减乘除最后都可归结为加法运算，因此加法器是核心。

全加器

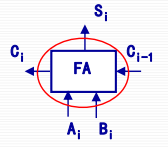
$\rm P_i$：传递进位，$\rm =A_i\oplus B_i$
$\rm G_i$：本地进位，$\rm =A_iB_i$

$\rm C_i=G_i+P_iC_{i-1}$

串行加法器

串行加法器并不是一串加法器串联，而是只由一个加法器，各位数据先后送入。

并行加法器

串行加法器速度很慢，主要原因是单个全加器需要$\rm A_i$和$\rm Bi$以及$\rm C\{(i-1)}$来产生此位结果，而进位信号是一级一级产生的，因此字长对延迟时间影响很大，进位信号称为全加器速度的主要瓶颈。

并行进位

速度很快但电路过于复杂。

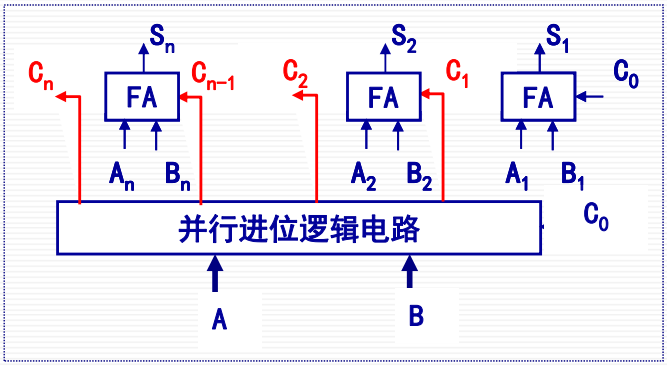
同一时间产生各级进位信号，然后每一个最小加法器单元得到进位信号后，获取该组输出。

分组并行进位

先行进位解决了各级进位信号逐步产生导致的加法器运算速度慢的问题。

单级先行进位

组内并行，组间串行

多级先行进位

组内并行，组间并行。

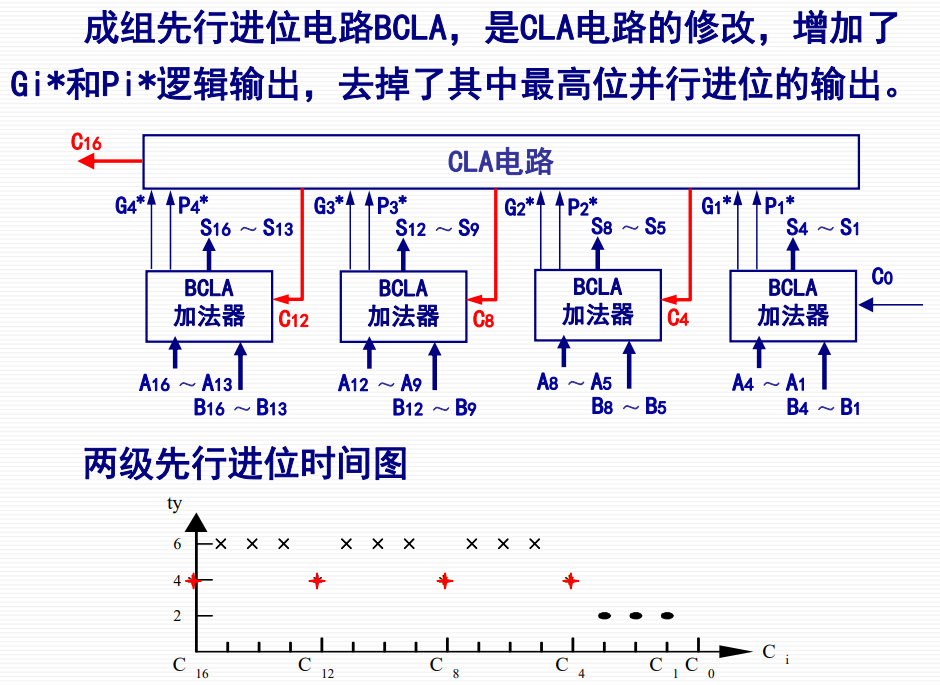
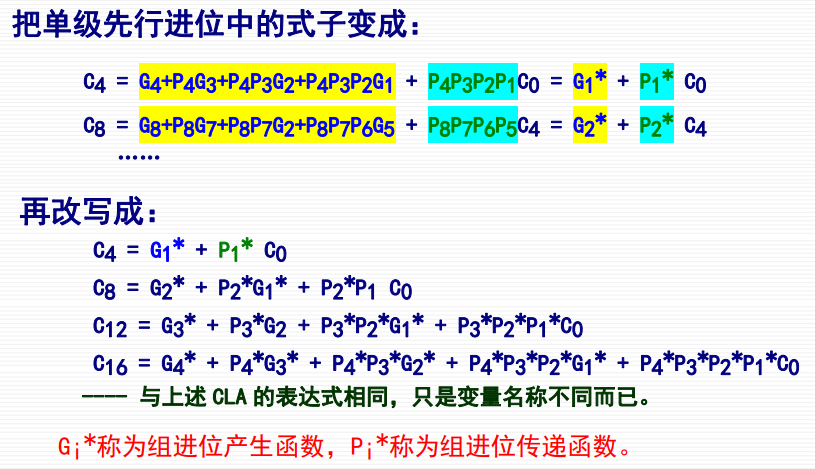
可见，组间进位函数可由组内各位决定，因此：

2ty内，产生第一组的$\rm C_1、C_2、C_3$及各组$\rm G_i^*$和$G_i^*$
4ty时，CLA电路通过传入的$G^$和$P^$产生各组的最低进位信号
6ty时，各组得到最低进位信号并产生组内各进位信号

定点加减运算

原码定点加法运算

减法则加原数原码的变补，如4位原码表示的十进制数-3变补后就成了5，此时某个数-3和+5的结果是一样的。

补码定点加减运算

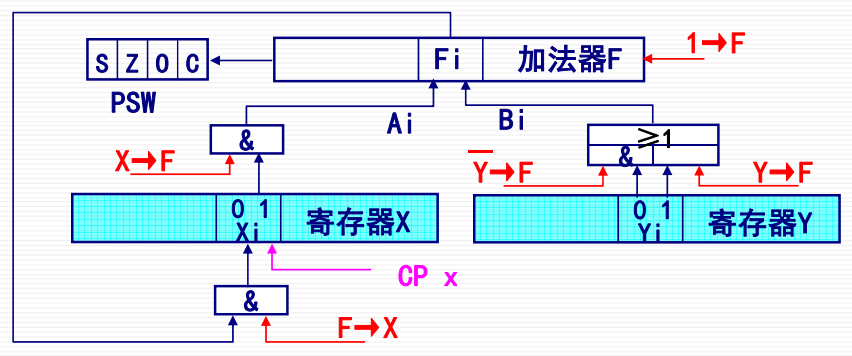
左侧与门控制左侧数字的输入
下方与门用来控制将运算结果存入寄存器X
提供$\overline Y\rightarrow$ 可以将补码取反输入加法器F，再提供$1 \rightarrow F$即可实现减法；提供$Y\rightarrow F$可以将补码输入加法器。（这个电路图右边Y寄存器那一坨我还看不懂……）

带符号数的移位和舍入操作

补码移位：符号位不变，左移时空位补零，右移时，正数空位补0，负数空位补1，原因见补码部分的原理说明。

算数移位功能的实现

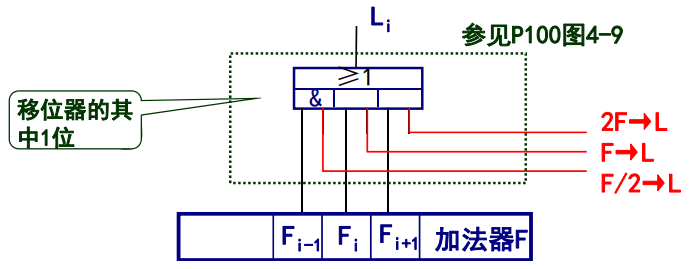
我看不懂……

该运算器无寄存功能，运算完后需要将其保存到寄存器当中。

其他移位

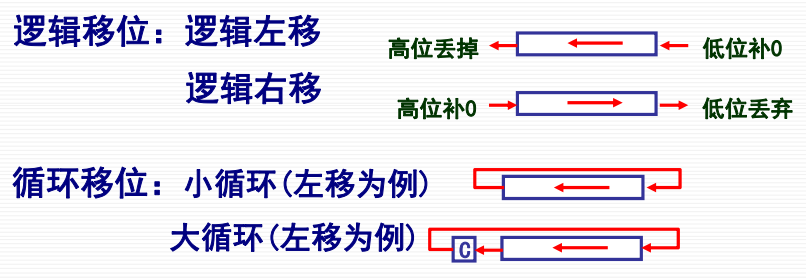
查表舍入法（待补充）

定点乘法运算

原码一位乘法

从列竖式手算演变而来。

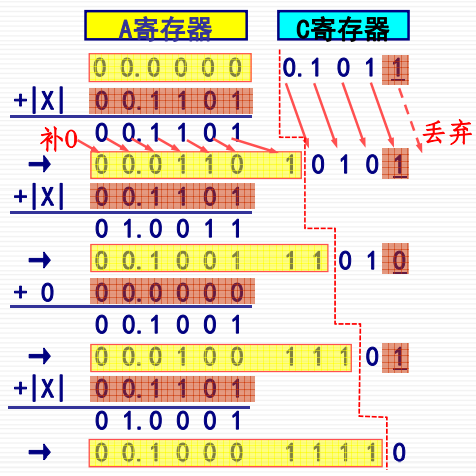
寄存器A：存放部分积以及最后结果的高位部分。
寄存器C：存放乘数以及部分积的低位部分。
寄存器B：存放被乘数。

每计算一次，A中的部分积和C中的乘数就一同右移一位。

补码一位乘法

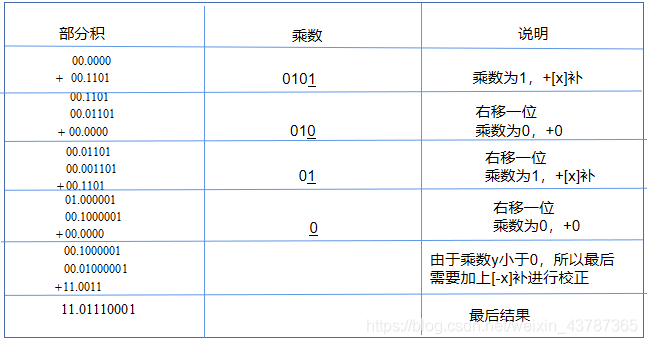
校正法

乘数$Y>0$时，按原码乘法进行运算，但移位规则按补码进行。
乘数$Y<0$时，去掉$[Y]_补$的符号位，按原码运算，最后加上$[-X]_补$
这是啥原理呢？我个人的理解是，因为在乘数$Y\leq 0$的时候，Y的补码最高位是负权，因此直接需要单独处理。在完成了对非符号位的乘法操作后，加上$[-X]_补$也就相当于是乘了负权。

https://blog.csdn.net/weixin_43787365/article/details/106423859

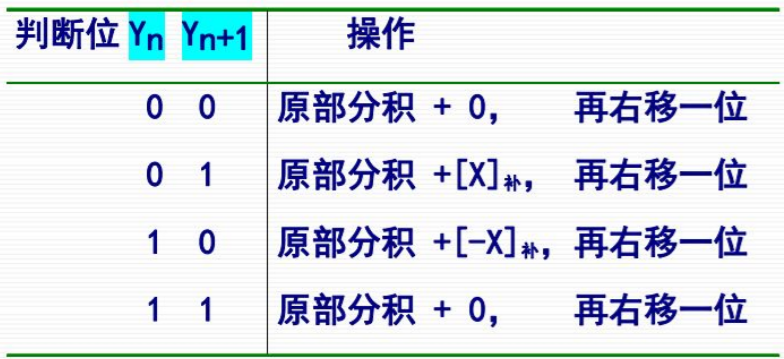
比较法

Booth夫妇利用校正法的统一表达式找到了补码乘法所得结果的从低位到高位的递推公式，统一了各种符号下的补码乘法操作，免去了校正步骤，简化了补码乘法电路。

定点除法运算

原码比较法和恢复余数法

这两种办法是非常直观、朴素的做法。比较法是在求商之前，将左移后的部分余数与除数比较大小，来决定商0还是商1；余数恢复法是不论部分余数减除数是否够减，都先减了再说，根据结果的正负来判断商，如果结果为负数，还需要重新把除数加回部分余数上。

原码加减交替法

基于恢复余数法，但免去了恢复操作。

不够减时$ri=2r{i-1}-Y$，而$r_{i+1}=2r_i+Y$
通式如下：$r_{i+1}=2r_i(1-2Q_i)\times Y$

注意，这里有一个补码的知识点，$[X]_原-[Y]_补=[X]_原+[-Y]_补$

规格化浮点数运算

对阶

让小阶向大阶对齐

阶码运算部件完成阶码加、减运算，并控制对阶和规格化时的阶码调整。

计算尾数

“尾数运算部件”完成尾数的四则运算，判断尾数是否规格化。

尾数规格化

溢出判断

“溢出判断电路”用双符号位判断阶码是否溢出。