整数
常用的有符号整数表示方法有原码、反码、补码。
原码
最高位为符号位。
反码
最高有效位权为$-(2^{w-1}-1)$
补码
最高位是符号位,同时也叫“负权”,权是$-2^{w-1}$
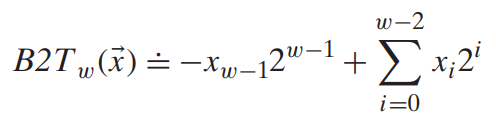
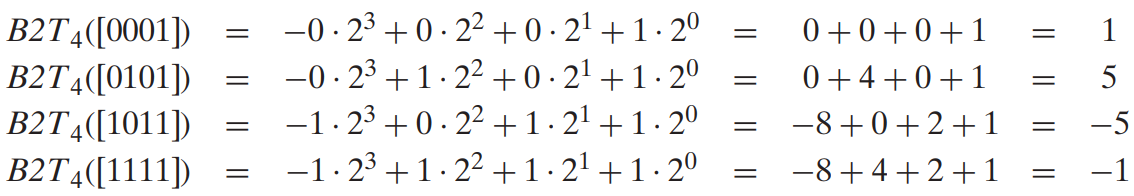
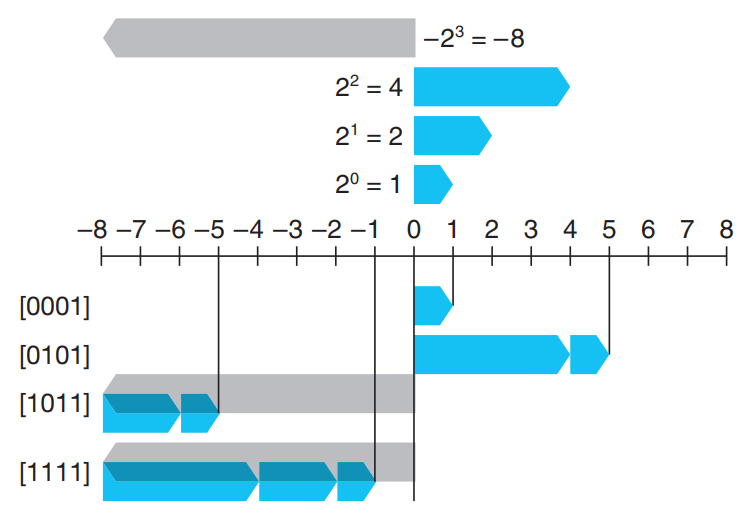
由以上定义可知,补码能表示的负数比正数多1,因为补码所能表示的最小负数是负权值,而能表示的最大正数是负权值的绝对值-1。可见补码的范围是不对称的。C语言标准规定的取值范围区间都是对称的,即不含补码表示的最小数$TMin$,因此为了保证程序的最大可移植性,不建议使用这个最小数。
变补

右移

左移

浮点数
$N=M\times r^E$
M是尾数
规格化浮点数
尾数M的绝对值取值范围:$\frac{1}{r}\leq \left| M\right|\textless 1$。
原因:要充分利用尾数有效位数,其原码符号位的后一位必须是1,即其真值的取值范围满足上式。
如果运算结果超出了编码所能表示的最大范围,即发生了溢出现象。
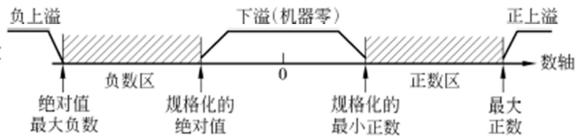
下溢即计算结果小于了可以表示的最小小数。
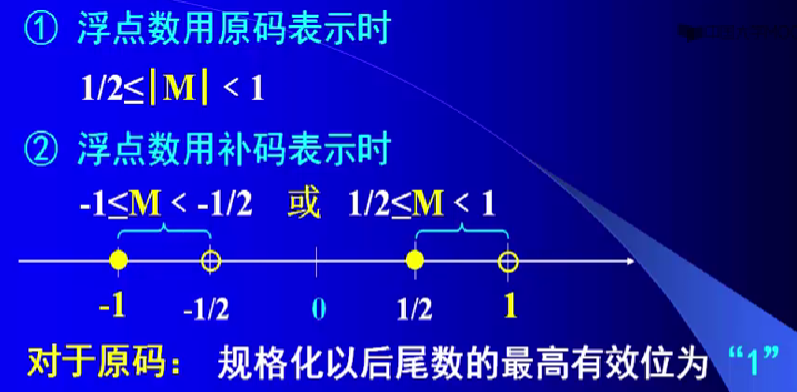
在补码表示时,若基数为2,则最高两位必须相异才是规格化的。
阶码的移码表示法
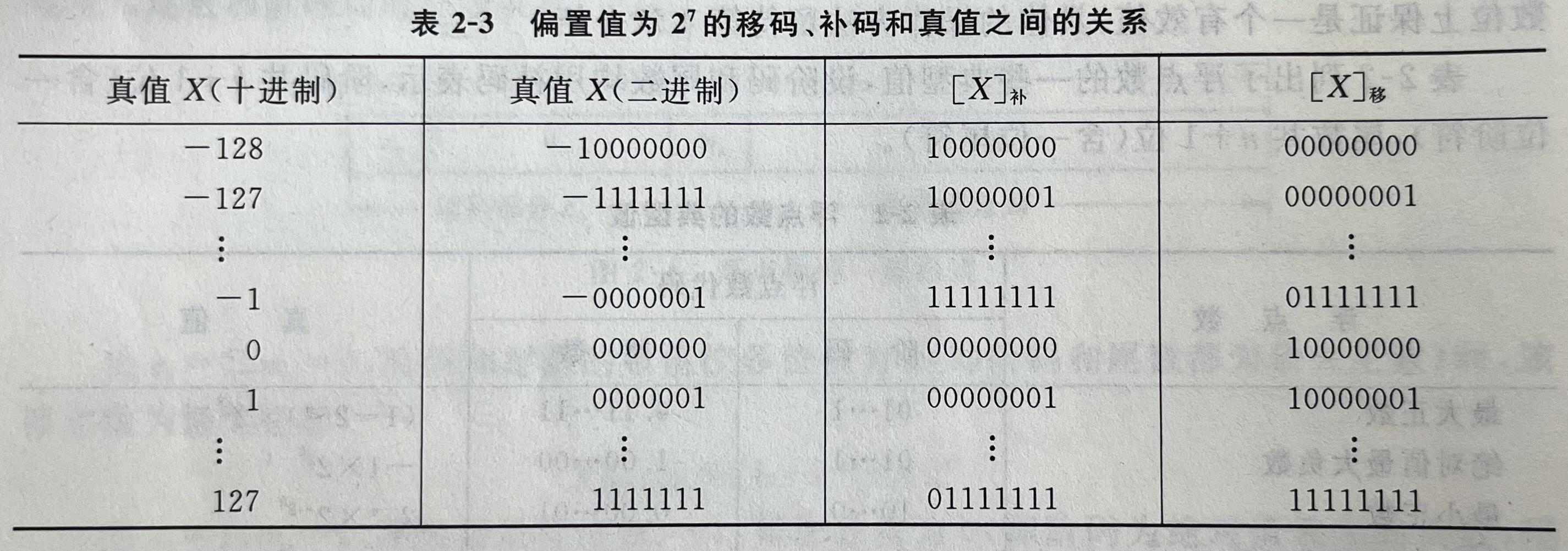
为了能简化浮点数阶码的大小比较,简化机器中的判零电路(让浮点数0的机器数全为0),用移码来表示浮点数的阶码。
具体操作方法是在真值$X$上加一个常数(偏置值),使数据的正负符号数字化。为了达到上一段所述的目的,偏置值需取$2^{n-1}$(后面所说的移码均指偏置值为$2^{n-1}$的移码),即让数字在数轴上整体向右平移$n$位(n为数字总位数),这样做能让原本的最小值变成1,而移码的每一位都为0时,表示的是$-2^n$,这与补码有些类似,在编码后,负数的表示位数多出了一位。即,原码的表示范围与补码一致。
为什么偏移值是$2^{n-1}$而不是$2^n$呢,因为8位二进制数最高位权重其实是$2^{n-1}$而非$2^{n}$。
要注意的是,假如用数轴表示阶码的真值$X$,原本的负半轴被移动到数轴的正半轴后,最高位为0的所有阶码所对应的就是原本在负半轴上的阶码,最高位为1的阶码所对应的就是原本在正半轴上的阶码。因此在移码中,最高位为0的为负值,最高位为1的为正值,这一点与之前的原码、反码、补码都不同。
尾数的基数
尾数的基数$r$一般取2或2的整次方,$r$的值越大:
- 可以表示的数的范围增大。
- 可表示的数的精度单调下降。
- 运算精度损失更低,因为较大的基数会减少尾数右移的次数。
- 运算速度更快,因为尾数移位次数变少。
- 可以表示的数字数量增加。
- 数在数轴上的分布愈发稀疏。
不太能理解为什么尾数的基数越大,它能表示的浮点数越多。因为尾数的位数确定之后,它能表示的数字数量也就确定了,基数的尾数变化,也只是让这些尾数所对应的真值一起变大变小,而不会改变所能代表的真值总数。Google后看到了一个解释:这一条仅在“规格化浮点数”的前提下成立。
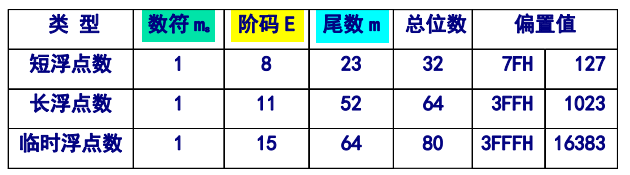
IEEE 754 标准浮点数
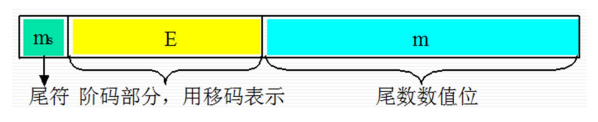
注意,尾数是用隐藏最高位的原码表示的,因此需要尾数符号位。
最高位为符号位,接下来是用移码表示的阶码,最后是尾数数值位。
- 阶码的移码,偏置值为$2^{n-1}-1$(n为位数)。
- 阶码全为0,表示负无穷;阶码全为1,表示正无穷。
- 尾数隐藏了最高位。例如$(1100)_2$规格化后为$1.1\times 2^3$,最高位的1将不被储存在尾数内。
非数值数据
十进制数和数串
十进制数的编码
用4位二进制来表示1位十进制数(BCD码)。
8421码
又叫NBCD码(Nature BCD),是有权码,最高位到最低位位权分别为'8 4 2 1`。
1010~1111是非法码
2421码
有权码,位权2 4 2 1。对9自补码,即按位取反可得对9补数,可简化运算电路。
0101~1010是非法码
余三码
8421码 + 3,也是对9自补码
Gray码
- 从一个代码到下一个代码,只有一位发生变化
- 首位两个码也只有一位不同,因此有循环性
由于以上特性,可以避免计数时发生中间错误。有不同的具体方案。
数串
非压缩的十进制数串
用ASCII码表示,前分割式将符号位单独放在前面一个字节,后嵌入式将符号信息加在最低数值位。由于ASCII中表示数字的部分只有后四位有区别,因此不利于数值处理,常用于非数值处理。
压缩的十进制数串
一个自己存两个BCD码来表示。
.
.
.
.
.
部分图片来自马永强老师的PPT,以及《Computer Systems, A Programmer's Perspective》