一个线性方程的推导
训练模型,让其推理出一组输入和输出间的关系
x值
-1.0, 0.0, 1.0, 2.0, 3.0, 4.0y值
-3.0, -1.0, 1.0, 3.0, 5.0, 7.0以上两组数据的关系是$y=2x-1$
代码实现
from tensorflow import keras
from tensorflow.keras import layers
import numpy as np # 导入NumPython
model = keras.Sequential(
layers.Dense(units=1, input_shape=[1])
) # units:层数,input_shape:输入值
model.compile(optimizer='sgd', loss='mean_squared_error')
# optimizer:衡量损失后,以优化函数继续
# loss:损失函数,衡量猜测结果的准确度
xs = np.array([-1.0, 0.0, 1.0, 2.0, 3.0, 4.0])
ys = np.array([-3.0, -1.0, 1.0, 3.0, 5.0, 7.0])
model.fit(xs, ys, epochs=100)
# epochs:训练次数
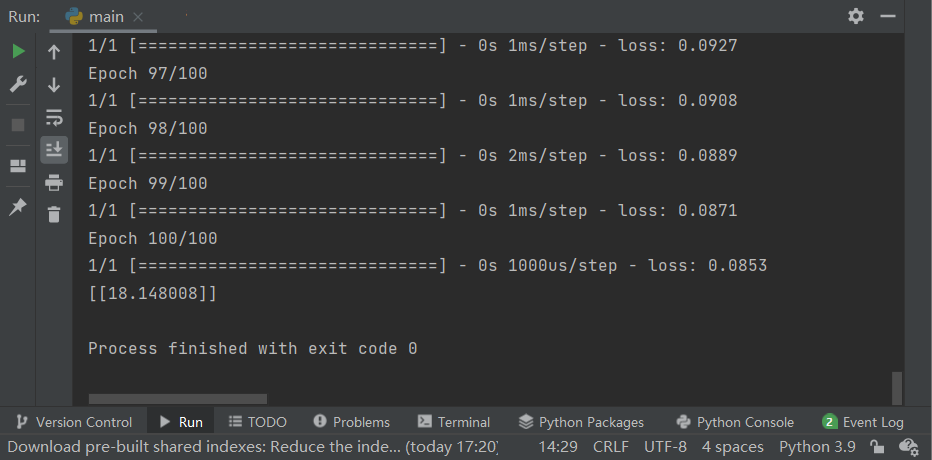
print(model.predict([10.0]))训练100次,10.0的预测结果是:17.567379
训练1000次,10.0的预测结果是:18.999897
训练10000次,10.0的预测结果是:18.999987
训练100000次,10.0的预测结果是:18.999987
上面这组数据说明了什么呢?说明在这个例子里,训练次数越多,预测结果越准确(废话hhh,其实只是第一次实现这个东西让我很兴奋,然后把唯一会改的一个参数改来改去玩玩罢了。)
fashion mnist 数据集
机器学习的
hello, world!
代码实现
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
fashion_mnist = keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
# 定义模型
model = keras.Sequential([
layers.Flatten(input_shape=(28, 28)), # 输入28*28的图片
layers.Dense(128, activation=tf.nn.relu), # 调参
# 128个计算函数(此处的“计算函数”并非准确术语)
# activation: 激活函数
# relu:线性整流函数,当数值大于零,则返回该数,否则返回零
layers.Dense(10, activation=tf.nn.softmax) # 输出0-10的编号
# softmax: 将一个数组中最大值修改为1,其他修改为0
])
# 编译模型
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy')
# 开始训练
model.fit(train_images, train_labels, epochs=10)准确度达94%
