吸收
溶解度曲线
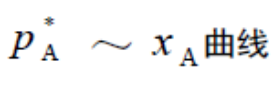
分别表示溶解速率等于逸出速率时的分压和摩尔分数

亨利定律
溶解度越大:
-
亨利系数$E$更小
-
溶解度系数$H$更大
-
相平衡常数$m$更小
-
$c_A^*=Hp_A$,即$H=\frac{c_A}{p_A^*}$,其中$c_A^*$是相平衡溶解度,$H$为比例系数
-
$E=\frac{C}{H}$
-
$p_A^*=Ex_a$
-
$m=\frac{E}{P}$
-
$C=\frac{\rho_L}{M_L}\approx\frac{\rho_s}{M_s}$,其中$\rho_L$是溶液密度,$M_L$是溶液摩尔质量,C是浓度。
吸收传质速率
- $K_y=\frac{1}{\left(\frac{1}{k_y}+\frac{m}{k_x}\right)}$
- $k_x=mK_y$,m是系数。
- 传质速率$N_A=K_y(y-y^*)$,$K_y$是气相总传质系数。
- 传质速率$N_A=k_y(y-y_i)$,y和$y_i$分别表示气相主体及相界面上的溶质摩尔分数。
- 气相阻力$\frac{1}{k_y}$,液相阻力$\frac{m}{k_x}$
双膜模型
- 易溶气体,液膜阻力 << 气膜阻力,如水吸收氨
- 难溶气体,气膜阻力 << 液膜阻力,如水吸收氧
蒸馏
气液平衡相图
温度-组成图
溶液平衡温度随组成而变化。
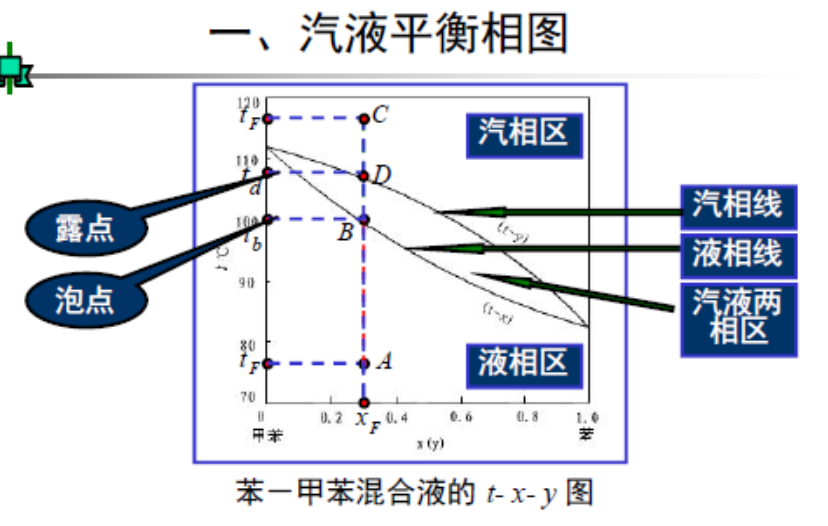
- 泡点:上方的曲线就是泡点线,往上就沸腾气化
- 露点:下方的曲线就是露点线,往下就凝结液化
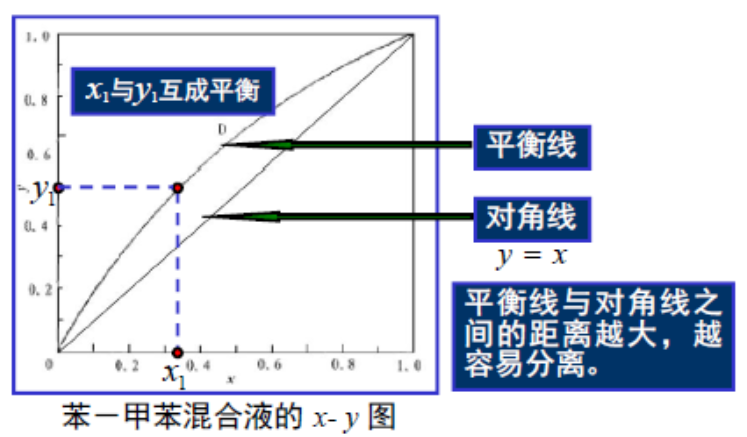
气-液组成图
一定压力下,处于平衡状态的气液两相组成的关系。
拉乌尔定律
理想溶液两相平衡时,溶液上方组分的分压与溶液中该组分的摩尔分数成正比。

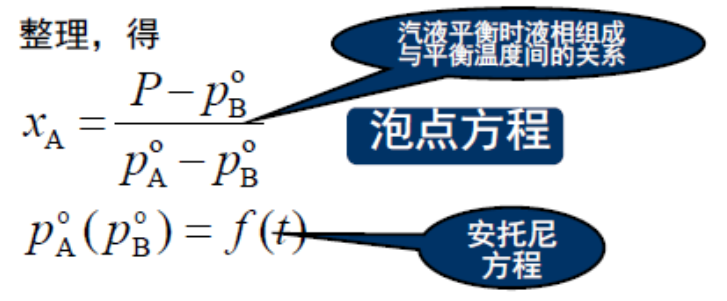
挥发度
挥发度定义
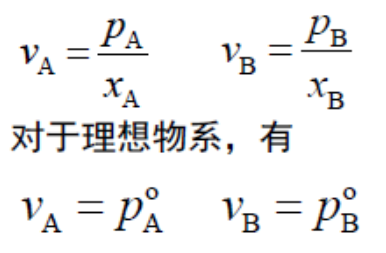
相对挥发度定义
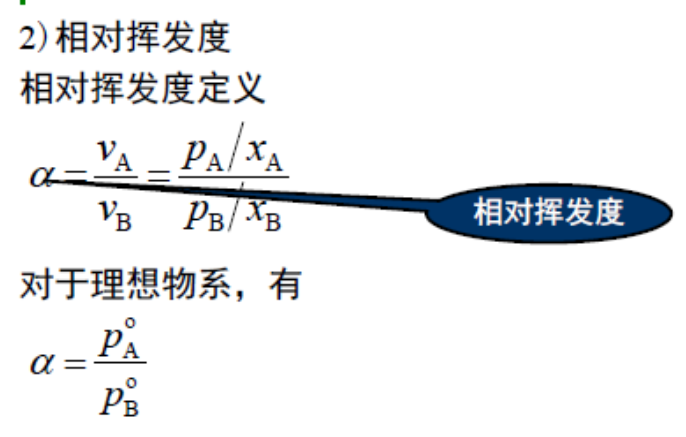
气液平衡方程


干燥
湿空气的性质
水蒸气含量表示方法
- 水蒸气分压:$\rm p_w=yP$(y为摩尔分数,P为总压)
- 湿度:$H=\frac{水汽质量kg}{绝干空气质量kg}=0.622\cdot\frac{p_w}{P-p_w}$(P为总压,$p_w$为水蒸气分压),单位$\rm kg\cdot kg^{-1}$
- 相对湿度:$\varphi=\frac{空气中水汽分压}{同温度下水的饱和蒸气压}=\frac{p_w}{p_s}\times 100\%$$p_s$需查表。
性质计算
- 湿比热容:$c_H=1.01+1.88H$,1kg绝干空气连同其所带的$H\rm kg$水蒸气升高1℃所需热量。单位$\rm kJ\cdot kg^{-1}\cdot K^{-1}$
- 湿空气的焓:$I=(1.01+1.88H)t+2492H=c_Ht+2492H 单位\rm KJ/kg$,热焓,单位$\rm kJ\cdot kg^{-1}$
- 湿比容:$V_H=0.773\times\left(\frac{P}{P-p_w}\right)\left(\frac{273+t}{273}\right)=(0.773+1.244H)\cdot \left(\frac{273+t}{273}\right)$,单位$\rm m^3\cdot kg^{-1}$
- 绝热饱和温度:$tas$,绝热饱和湿度$Has$,
$t=tas+\frac{ras}{C_H}(Has-H)$
湿度测定
干球温度
空气的真实温度
湿球温度$t_w$
大量不饱和空气与少量水长期接触后,水的温度。
露点
将不饱和空气在H不变的情况下进行冷却,达到饱和状态时的温度就是露点。此时开始有水珠冷凝出来。
湿空气饱和时,$p_w$为露点$t_d$下的饱和蒸气压$p_d$,对应的湿度是饱和湿度$H_d$。所以已知总压,就能通过H求出$p_d$以确定露点温度。
干球温度 $t \geq$ 湿球温度 $t_w\approx$绝热饱和温度$tas\geq$ 露点温度$t_d$ ,当空气为饱和空气时等号成立。